백트래킹이란 조건을 만족하는 경우를 탐색하는 방법입니다.
백 트래킹이라는 단어처럼 탐색하는 과정이 길을 찾고 되돌아가는 것과 비슷합니다.
한 번 예시를 들어봅시다.

1, 2, 3으로 만들 수 있는 세 자리 숫자를 모두 출력해야 합니다.
첫째 자리 - 둘째 자리 - 셋째 자리를 순서대로 결정한다고 가정하면, 경우를 트리로 표현할 수 있습니다.

각 자리를 1, 2, 3 순서로 선택하며 내려간다고 하면, 가장 처음 도착하는 숫자는 1-1-1입니다.
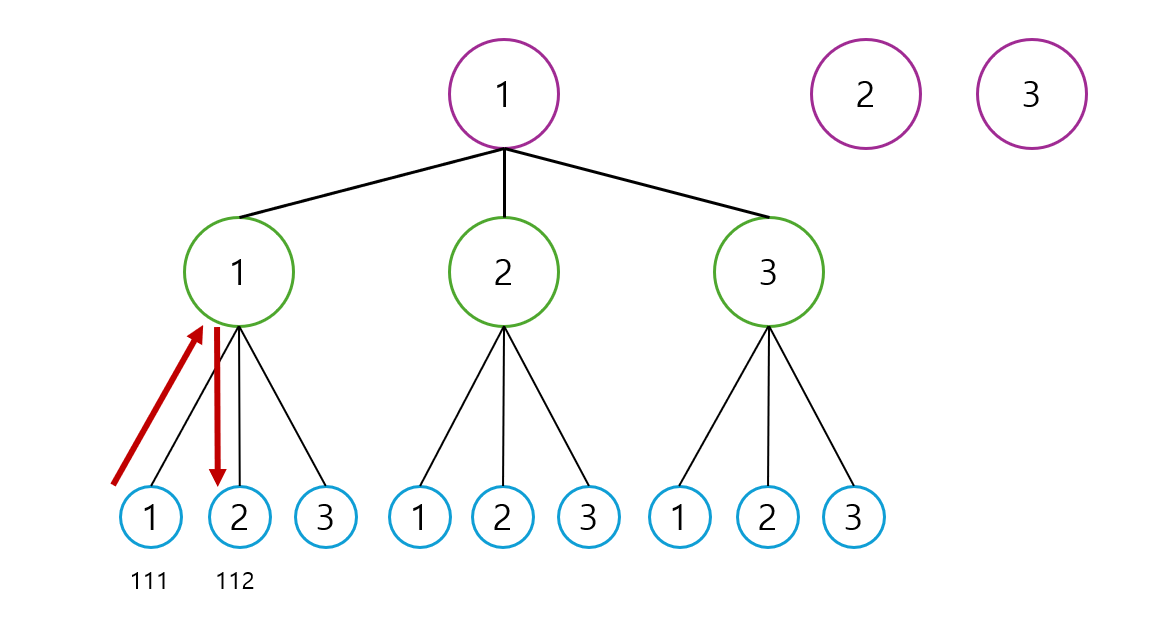
1-1-1로 트리의 끝에 도착했다면, 다시 1-1로 돌아가고(백 트래킹 하고) 이번에는 2를 선택합니다.

반복하면 모든 경우를 찾을 수 있습니다.
백 트래킹의 장점은
1. 가능한 경우를 탐색하면서도 가지치기로 경우의 수를 줄이기에 용이합니다.
만약 현재 단계에서 조건이 불가능하다면 다음 단계로 넘어갈 필요가 없습니다.
2. 다음 단계로 넘어가거나, 가지치기를 하는 과정에서 최적화를 할 여지가 있습니다.
종종, 가장 답일 가능성이 높은 경우를 선택해서 효율을 높일 수 있습니다.
백 트래킹을 사용하는 예로 순열을 만들거나, n-queen 문제가 있습니다.
문제를 하나 풀어봅시다.
15649번: N과 M (1)
한 줄에 하나씩 문제의 조건을 만족하는 수열을 출력한다. 중복되는 수열을 여러 번 출력하면 안되며, 각 수열은 공백으로 구분해서 출력해야 한다. 수열은 사전 순으로 증가하는 순서로 출력해
www.acmicpc.net
문제
1~N까지의 자연수 중 M개를 중복 없이 뽑아 나열한 수열들을 오름차순으로 출력하시오 (1<= N, M <= 8)
시도 1
가장 최악의 방법을 생각해 봅시다.
void solve1() {
for (int i = power10[M-1]; i < power10[M]; i++) {
if (is_valid(i)) {
print(i);
}
}
}
우선 순열을 하나의 수(123 -> (1 2 3))로 생각하고, 브루트 포스로 M자리 순열의 모든 경우에서 해당 숫자가 올바른지 검사합니다. is_valid()는 각 자리가 중복인지, N의 범위에 있는지 검사합니다.
작동은 하지만 필요 없는 경우를 너무 많이 검사합니다. 예를 들어 (9 9 9)는 N의 범위에 절대 들어갈 수 없지만 이를 거를 수단이 없습니다.
시도 2 - 반복문 사용
반복문을 통해 사용하는 사용하는 숫자의 범위를 1~N으로 좁혀보겠습니다.
void solve2() {
for (int i = 1; i <= N; i++) {
int numi = i;
if (M == 1 && is_valid(numi))
print(numi);
else
for (int j = 1; j <= N; j++) {
int numj = numi * 10 + j;
if (M == 2 && is_valid(numj))
print(numj);
else
for (int k = 1; k <= N; k++) {
// ......
for (int p = 1; p <= N; p++) {
int nump = numo * 10 + p;
if (M == 8 && is_valid(nump))
print(nump);
}
}
}
}
이제 (9 9 9 9)처럼 범위를 벗어나는 숫자를 검사하지 않습니다. 하지만 여전히 불필요한 검사가 이루어지고 있습니다. 예를 들어 앞의 순열 조합이 불가능하다면, 뒤의 경우는 무조건 불가능하기 때문에 검사하지 않아도 됩니다. 또한 반복문을 중첩하면 코드가 난잡해질뿐더러, M의 값이 커짐에 따라 코드를 추가해야 합니다.
시도 3 - 백 트래킹 사용
void solve3(int idx, int value, vector<bool> &is_used) {
// M의 끝에 도착
if (idx == M) {
print(value);
return;
}
for (int i = 1; i <= N; i++) {
if (is_used[i] == false) { // 중복 검사
is_used[i] = true;
int num = value * 10 + i;
solve3(idx + 1, num, is_used);
is_used[i] = false;
}
}
}
백 트래킹을 이용해 재귀함수로 만들어 봅시다. 함수는 idx를 통해 자신이 몇 번째 반복문에 있는지 확인합니다. 즉, 현재 함수는 다음 함수에서 idx를 하나 더해 재귀호출하고, 만약 idx == M 깊이 까지 도달하면 탐색을 종료합니다. 이제 M이 늘어난다고 해도 반복문을 더 중첩할 필요가 없습니다.
또한 vector<bool> is_used가 추가됐습니다. 현재 루프는 is_used를 확인하고, 사용하지 않은 숫자 하나를 뽑고, true로 체크한 뒤, 다음 함수에게 넘겨줍니다. 사용이 끝나면 다시 false를 넣어 다른 곳에서 사용할 수 있게 합니다. 이 방식을 사용하면 is_valid()로 체크할 필요 없이 숫자가 중복되는 경우를 제거할 수 있습니다. 즉, (1 1... 로 시작하는 경우를 처음부터 제외시킵니다.
재귀함수를 적절히 사용하면 원하는 깊이까지 탐색이 가능하고, 필요 없는 경우를 제거하기도 유용합니다.